Examples of numerical semi-continuous functions

Though we have been previously discussing the abstract definition of lower and upper semi-continuity, there are also tailored definitions for numerical functions, single-valued multifunctions which map into the extended real numbers. For the moment, let’s only consider these numerical functions \(\newcommand{\set}[1]{\{#1\}} \renewcommand{\bar}{... Read more 27 Jun 2018 - 4 minute read

Understanding semi-continuity of multifunctions

Let \(X\) and \(Y\) be topological spaces. One of the basic objects of study in topology are the continuous functions \(f : X \to Y\). Continuity in its pure form is a topological characterization: if \(V \subseteq Y\) is an open set, then continuity is equivalent to the openness of \(f^{-1}[V] \subseteq X\). The same concept is useful for multi... Read more 26 Jun 2018 - 4 minute read

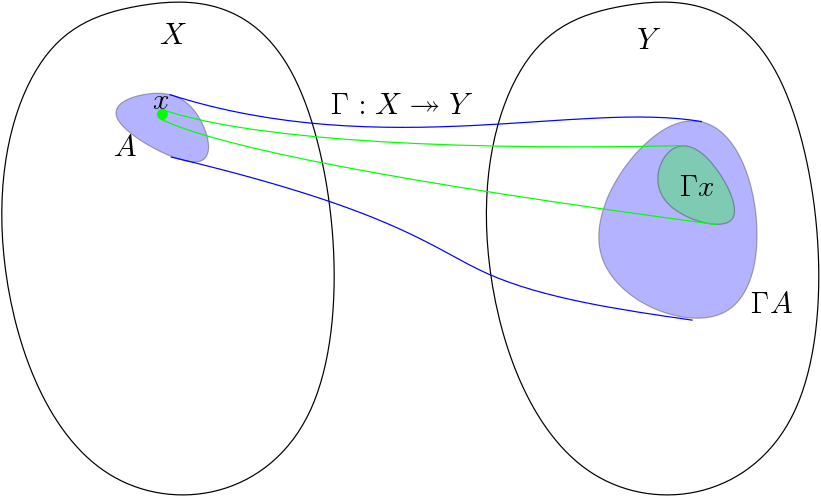
Multifunction inverses

When we deal with normal functions \(f : X \to Y\) we are frequently interested in the behavior of \(f\) on subsets of \(X\), rather than just elements. We might write \(f [ A ]\) to denote the image of \(f\) on the subset \(A \subseteq X\). Conversely, given a subset \(B \subseteq Y\), we can examine the “preimage” of \(B\) by \(f\) in the foll... Read more 06 Jun 2018 - 3 minute read

My summer excursion into multifunctions

Besides managing a course, my first summer goal is to understand the Berge maximum theorem (BMT). According to Wikipedia, the theorem is useful for describing continuity conditions for the solution of parameterized optimization problems. Since I’m still new to the whole subject, I don’t quite understand what that means! More on its interpretatio... Read more 05 Jun 2018 - 3 minute read

Reflections on the first year of graduate school

Courses Probably the biggest transition from the undergraduate (and particularly, liberal arts) experience and graduate work became apparent in the courses I took. Generally speaking, I never had a class with more than 30 students in college. Here, the norm has been (with one exception) at least that many. I’ve found it harder to engage with t... Read more 04 Jun 2018 - 6 minute read