Multifunction inverses

When we deal with normal functions \(f : X \to Y\) we are frequently interested in the behavior of \(f\) on subsets of \(X\), rather than just elements. We might write \(f [ A ]\) to denote the image of \(f\) on the subset \(A \subseteq X\). Conversely, given a subset \(B \subseteq Y\), we can examine the “preimage” of \(B\) by \(f\) in the following way:

\[f^{-1} [B] = \{ x \in X : f(x) \in B \}.\]

This is, to some extent, an abuse of notation because the function \(f^{-1}\) may not exist. Nevertheless there is no ambiguity, since when \(f\) is bijective (and consequently \(f^{-1}\) exists), we have

\[f^{-1} [\{ y \}] = \{ f^{-1} (y) \}\]

for all \(y \in Y\). That is to say, the preimage of the singleton \(\{ y \}\) corresponds to the inverse function applied to \(y\).

Upper and lower inverses

One interesting issue that arises with multifunctions is that the preimage actually disaggregates into two separate concepts. Given \(\Gamma : X \twoheadrightarrow Y\), we define the lower inverse of a set \(B \subseteq Y\) as

\[\Gamma^- B = \{ x \in X : \Gamma x \cap B \ne \emptyset \}\]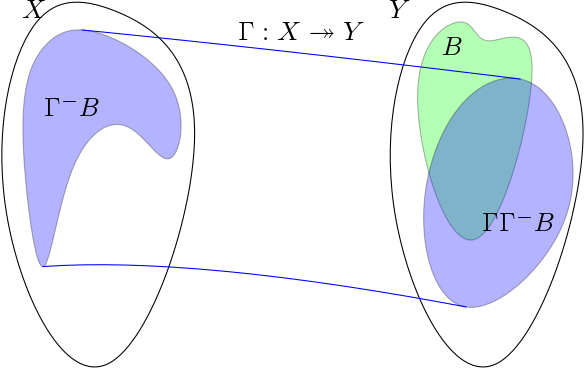

and the upper inverse as

\[\Gamma^+ B = \{ x \in X : \Gamma x \subseteq B \}.\]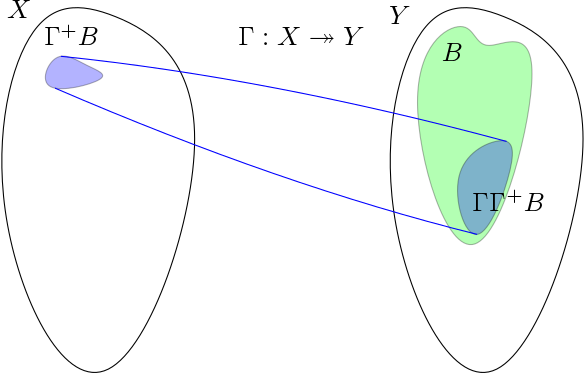

In English, the upper inverse of \(B\) is the collection of points in \(X\) which overlaps with \(B\) by \(\Gamma\), while the lower inverse of \(B\) is the collection of points which are mapped inside of \(B\) by \(\Gamma\). It is not hard to see that the upper inverse property is stronger than the lower inverse property. Indeed, \(\Gamma^+ B \subseteq \Gamma^- B\) for any \(B\).

As a sanity check, let’s verify that the upper and lower inverse images for single-valued multifunctions (i.e. functions) coincide. Let \(\sigma : X \twoheadrightarrow Y\) be a single-valued multifunction, and let \(B \subseteq Y\) be arbitrary. We know that \(\sigma^+ B \subseteq \sigma^- B\), so we just need to show that \(\sigma^- B \subseteq \sigma^+ B\). In that case, consider an arbitrary \(x \in \sigma^- B\). We know that \(\sigma x \cap B \ne \emptyset\), but since \(\sigma\) is single-valued, this means that

\[\{\sigma(x)\} \cap B \ne \emptyset.\]

In other words, \(\sigma x \subseteq B\), which implies that \(x \in \sigma^+ B\). In summary, for single-valued multifunctions, \(\sigma^+ = \sigma^- = \sigma^{-1}\), which is exactly the way we understand the preimage of a function.

Inverses as multifunctions

It is equivalent for a function \(f : X \to Y\) to have an inverse that \(f\) be bijective. This means that only a very small class of functions have inverses. Of course every function has its preimage, which resembles an inverse function, but since functions have considerable structure the preimage need not formally coincide with an inverse function.

By contrast, when we weaken our assumption that our mappings have unique outputs (i.e., when we go from functions to multifunctions), the distinction between preimages and inverse multifunctions disappears. That is, given \(\Gamma : X \twoheadrightarrow Y\), the multifunctions \(\Lambda, \Upsilon : Y \twoheadrightarrow X\) by

\[\Lambda y = \Gamma^- \{ y \}, \qquad \Upsilon y = \Gamma^+ \{ y \}\]

are perfectly well-defined. (Caveat: sometimes, \(\Lambda y\) and \(\Upsilon y\) can be empty. This does not contradict the definition of a multifunction.)

Inverses and continuity

Where are we headed with all of this? Recall that a function \(f : X \to Y\) is continuous if and only if \(f^{-1} [G]\) is open whenever \(G\) is open. But as we shall see, there are actually two notions of continuity embedded here: lower and upper semi-continuity. When we disaggregate, we will see that lower semi-continuity has a characterization in terms of the lower inverse and upper semi-continuity has a characterization in terms of the upper inverse. In the special case when both notions coincide, we arrive back at the usual criterion.

Published on June 6th, 2018 by David Kraemer