My summer excursion into multifunctions

Besides managing a course, my first summer goal is to understand the Berge maximum theorem (BMT). According to Wikipedia, the theorem is useful for describing continuity conditions for the solution of parameterized optimization problems. Since I’m still new to the whole subject, I don’t quite understand what that means! More on its interpretation and applications (hopefully!) soon.

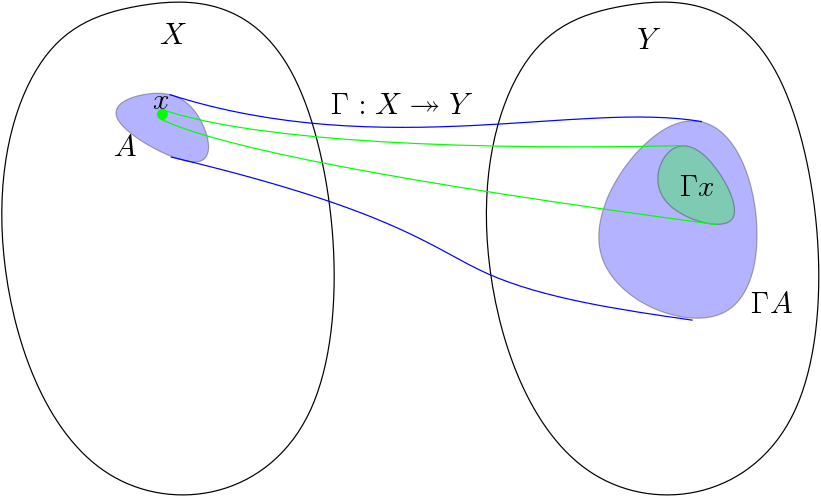
As a result in analysis, the BMT is novel to me because it relies on the notion of a multifunction (the translation of Berge’s text¹ calls it a correspondence). Intuitively, a function \(f : X \to Y\) assigns to each \(x \in X\) the value \(f(x) \in Y\). As you might expect, a multifunction \(F : X \twoheadrightarrow Y\) assigns a set of values to each \(x\). In other words, \(F(x) \subseteq Y\). There is a natural way to express this as a function by changing the codomain: define \(f : X \to 2^Y\) with \(f(x) = F(x)\), where \(2^Y\) denotes the power set of \(Y\). Nevertheless, it is useful to think of multifunctions as separate objects than functions, and that is how we will proceed.

A simple example of a multifunction is the square root operation: since both 2 and -2 are square roots of 4, we can define \(\sqrt{\cdot} : \mathbb{R}^+ \to \mathbb{R}\) that takes \(\sqrt{4} = \{-2,2\}\), for example. “Inverse” trig functions are, properly speaking, multifunctions: to see this, note the example that \(\sin^{-1}(0) = \{ \pi n : n \in \mathbb{Z}\}\). This is because we of course know that \(\sin(\pi n) = 0\) for all \(n \in \mathbb{Z}\).

Here I will adopt the notation of Berge’s book. He reserves capital Greek letters for general multifunctions and uses lower case Greek letters for the usual single-valued functions. The shorthand \(\Gamma x = \Gamma(x)\) and \(\Gamma A = \bigcup_{x \in A} \Gamma x\) will be of particular use.

There are a number of simple operations and results you can establish about multifunctions, but as a taste, I give one example. Suppose that we have two different multifunctions \(\Gamma_1, \Gamma_2 : X \twoheadrightarrow Y\). We can define a new mapping \(\Gamma_1 \cap \Gamma_2 : X \twoheadrightarrow Y\) which is given by

\[(\Gamma_1 \cap \Gamma_2) x = \Gamma_1 x \cap \Gamma_2 x.\]

Since multifunctions map to sets, it is actually very natural that we may want to construct new multifunctions by using the standard set operations. Indeed, there are many such common constructions. Let’s say that a multifunction \(\Gamma\) is injective if whenever \(x \ne x'\) we have \(\Gamma x \cap \Gamma x' = \emptyset\). (If you think through this definition, you will notice that an injective multifunction determines a partition of its range, i.e. implicitly defines an equivalence relation.) Here’s a neat fact that follows from the definition of a multifunction and some properties of set operations:

Proposition. If \(\Gamma_1, \Gamma_2 : X \twoheadrightarrow Y\) are multifunctions, and if \(\Gamma_1\) is injective, then so is \(\Gamma_1 \cap \Gamma_2\).

Proof. Let \(x \ne x'\). Then

\[\begin{align} (\Gamma_1 \cap \Gamma_2) x \cap (\Gamma_1 \cap \Gamma_2) x' &= (\Gamma_1 x \cap \Gamma_2 x ) \cap (\Gamma_1 x' \cap \Gamma_2 x') \\ &= (\Gamma_1 x \cap \Gamma_1 x') \cap (\Gamma_2 x \cap \Gamma_2 x') \\ &= \emptyset \cap (\Gamma_2 x \cap \Gamma_2 x') \\ &= \emptyset, \end{align}\]

as was needed. \(\square\)

From my first investigation, it seems that the power of the multifunction concept is that encapsulates sets. The above proof is an example of this, where the entire result boils down to properties of setwise operations. But it is also “close enough” to functions that it still yields many of their properties. Of note, which is particularly relevant to the BMT, one can discuss the continuity of multifunctions. This is ultimately where my exploration is heading.

Published on June 5th, 2018 by David Kraemer